Alan

.As Melody often notes, it can be useful to plot these sort of probabilities against each other.  Consider x_1 and x_2:

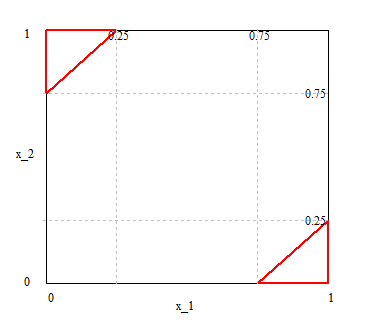
The probabilities of the pair can be thought of as uniformly randomly scattered points within a unit square.

The only regions of the square in which the lengths between the two values are greater than 3/4, are within the two red triangles indicated in the image above.

The probability that the lengths are greater than 3/4 is therefore given by p = Area of triangles/Area of square

The same probability holds for the lengths between x_3 and x_4, so, because the two probabilities are independent, the overall probability is given by p^2.

I'll leave you to do the number crunching.

You need to specify what you mean by "practical" domain.  The mathematical domain is -infinity to +infinity, so your use of "practical" suggests you have some limits on the values of V(x) (which we don't know).

@ bingboy

There's a sign wrong here:  (3x + 4y) + (3y - 4x)i = 1 - 8i

Hmm.  Look at the following:

Some checking is in order bingboy!

See if this helps:

Look at the diagram:

Find angle \(\alpha \) using the cosine rule    (i.e. \(cos(a) = (b^2 + c^2 - a^2)/(2bc)\) )

Take the ratio of the arc of the circle subtended by \(2\alpha \)  to that of the circumference of the whole circle to get the probability.

i.e. probability = \(2\alpha / (2\pi) \)

(Note that the lower point could be on the opposite side of the circle hence \(2\alpha \) not just \(\alpha \))

Like this (assuming my simplification of the numbers is correct):

I'll leave you to solve the above to find the actual value of Cfixed.

Hmm!  Check the left-hand side of 15f = 5m

As follows:

The following is one possibility: