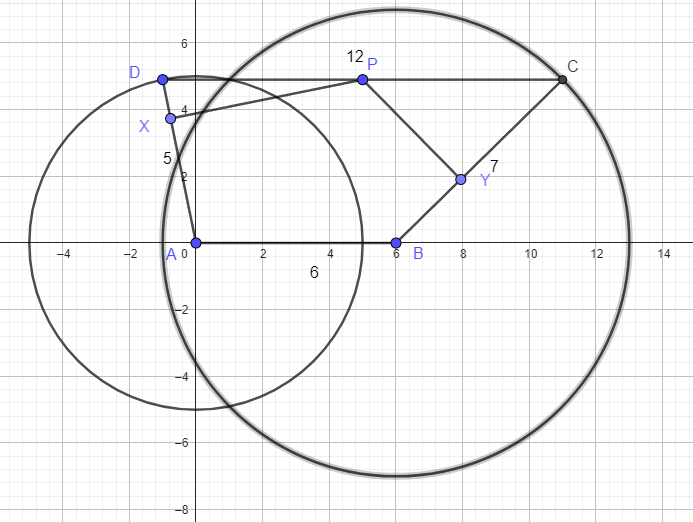
Let
A =(0,0)
B =(6,0)
Construct a circle centered at A with a radius of 5 and a circle centered at B with a radius of 7
If we let the x coordinate of D = -1 we can find the y coordinate as
(-1)^2 + y^2 = 25
y^2 = 24
y = 2sqrt (6)
Letting the x coordinate of C = 11, we can find the y coordinate as
( 11 - 6)^2 + y^2 = 49
5^2 + y^2 =49
y^2 = 24
y = 2sqrt (6) ( which we would expect )
Since CP / PD = 1
Let P = ([11 -1) /2, 2sqrt 6) = (5, 2sqrt 6 )
The slope of the line through AD = [ 2sqrt 6] / -1 = -2sqrt 6
And the equation of this line is y = (-2sqrt 6)x
In standard form we have (2sqrt6)x + y = 0 (1)
The slope of the line through BC = [ 2sqrt 6 - 0] / [ 11 - 6] = (2/5)sqrt 6
And the equation of the line through BC is y = (2/5)sqrt 6 ( x - 6) =
y =(2/5)sqrt (6)x - (12/5)sqrt 6
In standard from we have (2/5)sqrt (6)x -y - (12/5)sqrt (6) = 0 (2)
The formula for the distance between a point and a line is given by
abs [ Ax + By + C ] / sqrt [ A^2 + B^2 ] where (x,y) are the coordinates of the point
So using (1) , the distance from P to the line through AD = PX is
abs [ (2sqrt (6) (5) + 2sqrt (6) ] / sqrt [ (2sqrt (6))^2 + 1^2 ] = [12sqrt (6)] / 5
Likewise, the distance between P and the line through BC = PY is
abs [ (2/5)sqrt (6) (5) - 2sqrt (6) - (12/5)sqrt (6) ] / sqrt [ [(2/5)sqrt (6) ]^2 + 1^2 ] =
[ (12/5)sqrt 6] / (7/5) = [12sqrt (6)] / 7


