CPhill

AC will have the greatest length when angle  ABC = 90°

So

AC =  sqrt ( AB^2 + BC^2)  = sqrt ( 5^2 + 5^2)  = sqrt 50  =  5sqrt 2

We can  find the length of any edge  as

sqrt ( 3^2 + ^2)  =  sqrt (18)

The area of one face of the octahedron  =

(1/2) (sqrt 18)^2  sqrt (3) / 2 =  (9/2)sqrt 3

So....the total surface area =  8 * (9/2) sqrt 3  =   36sqrt 3

See the following

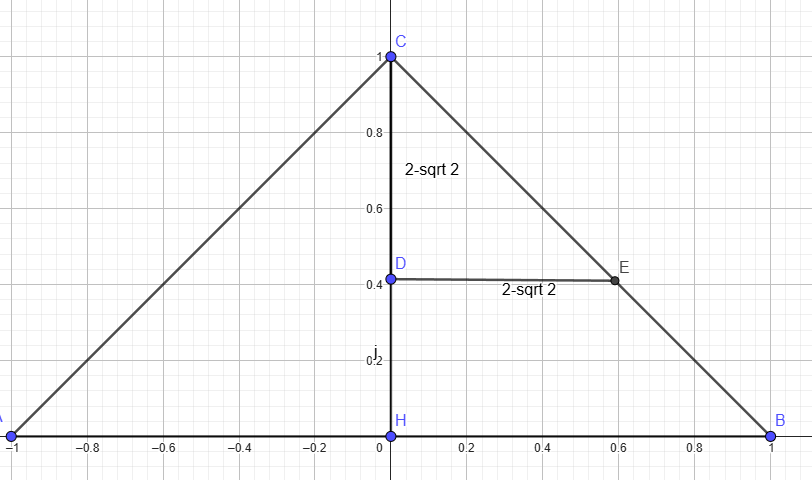
Triangle CDE similar to triangle CHB

CH = HB

So CD = DE

The radius of the smaller cone, DE  = its height, DC

Call these, x

Volume of smaller cone =  (1/3) base^2 * height = (1/3) pi * x^3

Volume of frustum  =   pi (1-x) (1 + x^2 + x) / 3  

Lateral Surface area of  smallercone =  pi * x * L 

L = slant height of smaller cone =  sqrt ( x^2 +  x^2) =  sqrt 2 * x

pi * x * sqrt (x^2 + x^2)  =   pi*  sqrt 2  * x^2

Lateral surface area of large cone  = pi * 1 * sqrt ( 1 + 1) =  pi * 1 * sqrt (2) = pi* sqrt 2

Surface area of frustum = lateral surface area of large  cone - lateral surface area of smaller cone  plus area of base of large cone = 

pi * sqrt 2 - pi sqrt 2 * x^2  =     pi *sqrt 2 * (1 -x^2)

plus area of circular base = pi * 1^2  = pi 

pi sqrt 2 * (1-x^2) + pi  =

pi [sqrt 2 * ( 1 -x^2) + 1]

So we have  the ratio of the volumes = 

[ (1/3) pi * x^3] / [  pi(1-x) (x^2 + x + 1 )/3 ] =  [   x^3 ]/ [ (1-x)(x^2 + x + 1)]   =  M

Ratio of surface areas =

[pi *sqrt 2 * x^2] / [ pi * sqrt 2 *(1-x^2) + pi]  =  [sqrt 2 * x^2 ] / [ sqrt2 * (1-x^2) + 1]  = N

Set M = N and solve for x     { let WolframAlpha  do the heavy lifting here !! }

x= 2 -sqrt 2 =  height of small  cone

Height of A to Height of C =  ( 2  - sqrt 2 ) / 1  =   2 -sqrt 2 

Here's my best attempt ???

If we "unroll" the cone we have the following triangle, ADB

Circumference of the cone = triangle base =  2pi * radius of cone =    2pi * 10  = 20 pi  = AB 

So

A =  (-10pi , 0)

B = (10pi , 0)

D = height of the cone  = (0, 20)

C = (5pi ,10)

The shortest distance from A to C   =  sqrt [(-10 pi -5pi)^2 + ( (20 -10)^2] = 

sqrt [ 225pi^2 + 100] ≈  48.17

Lateral surface area = pi * r * slant height

100 = pi * 12  * slant height

Slant height =  100 / (12 pi) =  25/ ( 3pi)

Height of the cone  =  sqrt [ slant height ^2 - radius^2 ] =   sqrtt [ (25/(3pi))^2 - 12^2] ≈  11.7

Volume of cone =

(1/3) h * pi * r^2  =

(1/3)(11.7)*pi (12)^2  ≈ 1764.3 u^2

Looking at a cross-section along the diagonal of the cube

Let the side of the cube = S = EF

The length of the bottom diagona of the cube  =  sqrt 2 *S = HF

We can construct similar triangles AFE  and ADC

AF / EF  =  AD / DC

DF = sqrt 2*S / 2 =  S/sqrt 2

So AF = 3 - S/sqrt 2

So we have

[ 3 -S/sqrt 2 ] / S =  3/6

[ 3 - S/sqrt 2 ] / S  = 1/2

2 [ 3 - S/sqrt 2] = S

6 - sqrt 2 * S = S

6 = S + sqrt 2*S

6 = S ( sqrt 2 + 1)

S = 6 / ( sqrt 2 + 1) =    6  (sqrt 2 - 1) = side of the cube 

See the following

Let circle A have a radius of 9   and let the small circle have a radius , r

Triangle ACD is right with

AC =the hypotenuse = 9 + r

AD is a leg = 9

DC is another leg = 9 -r

So we have this relationship

9^2 + ( 9 - r)^2  = (9 + r)^2

81 + 81 -18r + r^2  =  81 + 18r + r^2     simplify

81 =  36r

r  =  81/36  =  9/4  = the radius of the small circle

Let the circle have a radius of 4

Let A = (0,4)

Let B =  ( 2sqrt 3 , -2 )

AB = sqrt [ (2sqrt 3)^2 + (4--2)^2] = sqrt 48 = 4sqrt (3)  side length of triangle

MC = = (1/2) side length = 2sqrt 3

MB = side length * sqrt 3 =  2 sqrt 3 * sqrt 3 =  6

MB /MC  =  6 / [ 2sqrt 3]  =  3 /sqrt 3 =  sqrt 3

Each term   will  be -1 < term value  < 0

So the floor for each will be -1

Sum = 1000 (-1)  = -1000

r =  .016 / .4  =  .04

Sum  =     .016 / [ 1 -.04] =  .016 / .96  =  1/ 60