A diagram would be of great assistance for this problem, so I created one for you. I added lines and points where I saw fit to add clarity to the diagram:
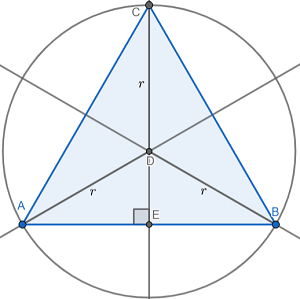
In order to find the area of any triangle, we need the length of the base and the length of the perpendicular height (also known as the altitude) of the triangle. Then, we can apply the formula \(A_{\triangle ABC}=\frac{1}{2}bh\) to find the area. In the diagram above, \(\overline{AB}\) represents the base, and \(\overline{EC}\) represents the perpendicular height of the triangle.
\(m\angle ADB=120^{\circ}\)as each central angle \(\triangle ABC\) forms divides equally in thirds. By inserting an angle bisector of \(\angle ADB\), this means that \(m\angle ADE=60^{\circ}\). This angle bisector also happens to be a perpendicular of chord \(\overline{AB}\). Combining all of this information together means that \(\triangle ADE\) is a 30-60-90 triangle.
A 30-60-90 triangle has a constant ratio of its sides of \(1:\sqrt{3}:2\). In this particular case, \(r\) is the length of the hypotenuse of \(\triangle ADE\). Let's use these ratios to find the length of the base and the height in terms of \(r\).
| \(\frac{AE}{r}=\frac{\sqrt{3}}{2}\\ AE=\frac{\sqrt{3}}{2}r\) | \(\frac{DE}{r}=\frac{1}{2}\\ DE=\frac{1}{2}r\) |
By parallel reasoning, \(BE=\frac{\sqrt{3}}{2}r\).
We can find \(AB\), the length of the base of the triangle in terms of r now.
\(AB=AE+BE\\ AB=\frac{\sqrt{3}}{2}r+\frac{\sqrt{3}}{2}r\\ AB=\sqrt{3}r\)
Similarly, we can do the same for \(CE\), the length of the perpendicular height of the triangle.
\(CE=CD+DE\\ CE=r+\frac{1}{2}r\\ CE=\frac{3}{2}r\)
Finally, let's solve for the area of the inscribed triangle in terms of r.
\(A_{\triangle ABC}=\frac{1}{2}*AB*CE\\ A_{\triangle ABC}=\frac{1}{2}*\sqrt{3}r*\frac{3}{2}r\\ A_{\triangle ABC}=\frac{3\sqrt{3}}{4}r^2\)
.This question took me over an hour to solve, but I can now share my findings with you! I am making the assumption that you meant triangles AXB and AXC in place of APB and APC. It is quite algebra-intensive. If this is not what you meant, then I wasted a long time of my day today :(
I created a diagram, and I added line segments and circles where I found necessary. I realize that the diagram is quite large and cluttered. Here it is below:
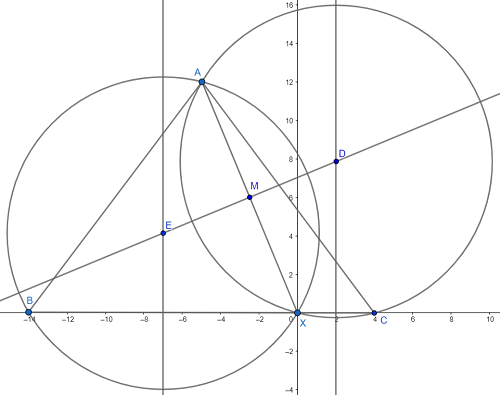
I will be utilizing coordinate geometry for this problem. With the diagram in its current orientation, I know that B=(-14,0) and X=(0,0) and C=(4,0). This way, I know the length of the base of \(\triangle ABC\) is 18. The only coordinate I need now is the y-coordinate of point A because that is the height of \(\triangle ABC\). Finding the area of the triangle is trivial at that point. Unfortunately, finding this coordinate is not so easy.
Since I don't know what the y-coordinate of point A, and I do not see an easy way to find the y-coordinate (or even the x-coordinate) of point A, I will denote them with variable letters. Let a = the x-coordinate of point A, and let b = the y-coordinate of point A. It would be nice if there was a way to relate a and b together, and I see one way of doing that. Since \(XA=13\), I can use the distance formula to relate a and b together like so:
\(d^2_{XA}=(a-0)^2+(b-0)^2\\ 13^2=a^2+b^2\\ b^2=169-a^2\\ b=\sqrt{169-a^2}\)
b is now written in terms of a, but now I am going to introduce a theorem that seems unrelated. That theorem states the following: The perpendicular bisector of a chord of a circle passes through the center of that circle. I have slyly used that theorem to my advantage here. \(\overline{AX}\) is a chord of both circumcircles of \(\triangle ABX\) and \(\triangle ACX\). \(\overleftrightarrow{ED}\) is the perpendicular bisector of \(\overline{AX}\), which, by the theorem I just stated, also pass through the circumcenters of both triangles.
We can find the slope of \(\overline{AX}\) and then use the properties of perpendicular line to find the slope of \(\overleftrightarrow{ED}\).
\(m_{\overline{AX}}=\frac{b}{a}\\ \therefore m_{\overleftrightarrow{ED}}=\frac{-a}{b}\)
But we can do more than that! Point M on the diagram represents the midpoint of \(\overline{AX}\), and we can find those coordinates in terms of a and b, too.
\(M=(\frac{a}{2},\frac{b}{2})\).
But we can do more that that, too. We can now derive an equation of \(\overleftrightarrow{ED}\) because we know the slope of the line and one point of the line. I will use point-slope form to start and simplify as much as possible from there.
| \(y-\frac{b}{2}=\frac{-a}{b}(x-\frac{a}{2})\\ y=\frac{-a}{b}x+\frac{a^2}{2b}+\frac{b}{2}\\ y=\frac{-2a}{2b}x+\frac{a^2}{2b}+\frac{b^2}{2b}\\ y=\frac{-2ax+a^2+b^2}{2b} \) | I substituted in \(169-a^2\) for \(b^2\) because I noticed that there would be some nice cancellation. |
| \(y=\frac{-2ax+a^2+(169-a^2)}{2b}\\ y=\frac{-2ax+169}{2b}\) | I decided not to simply further than this, at least for now. |
Remember that theorem I mentioned earlier? Yeah, we are using that one again. \(\overline{BX}\) is a chord of circle E, so E's center lies on its perpendicular bisector, which also lies on the line \(x=-7\). By parallel reasoning, circle D's center lies on \(x=2\). Let's use this newly discovered information to our advantage again!
| \(y_E=\frac{-2a*-7+169}{2b}\\ y_E=\frac{14a+169}{2b}\) | \(y_D=\frac{-2a*2+169}{2b}\\ y_D=\frac{-4a+169}{2b}\) |
We now know the x- and y-coordinates of the both circumcircles, so we can use the distance formula to write an expression for both radii.
| \(d_{\overline{EX}}=r_E\\ d_{\overline{EX}}=\sqrt{(-7-0)^2+(y_E-0)^2}\\ d_{\overline{EX}}=\sqrt{49+y^2_E} \) | \(d_\overline{DX}=r_D\\ d_\overline{DX}=\sqrt{(2-0)^2+(y_D-0)^2}\\ d_\overline{DX}=\sqrt{4+y^2_D}\) |
Conveniently, both radii are of the same length, so we can set the distances we just found equal to each other. We will finally be able to isolate a variable. How exciting! At this point, the rest is simply a test of your algebraic finesse. For an added challenge, I decided to avoid the use of a calculator.
| \(\sqrt{49+y^2_E}=\sqrt{4+y_D^2}\\ 49+y^2_E=4+y^2_D\\ 45+y^2_E=y^2_D\) | Let's subsitute in the corresponding expressions for \(y_E\) and \(y_D\). |
| \(45+\left(\frac{14a+169}{2b}\right)^2=\left(\frac{-4a+169}{2b}\right)^2\\ 45+\frac{196a^2+2*169*14a+169^2}{4b^2}=\frac{16a^2-2*169*4a+169^2}{4b^2}\\ 180b^2+196a^2+28*169*a+169^2=16a^2-8*169*a+169^2\\ 180(169-a^2)+196a^2+28*169*a=16a^2-8*169*a\\ 45(169-a^2)+49a^2+7*169*a=4a^2-2*169*a\\ 45*169-45a^2+45a^2+7*169*a=-2*169*a\\ 45*169+7*169*a=-2*169*a\\ 45+7a=-2a\\ -9a=45\\ a=-5\) | We finally solved for a. Yes, I checked if the value for a seems reasonable, and it certainly does. |
| \(b=\sqrt{169-a^2}\\ b=\sqrt{169-(-5)^2}\\ b=12\) | |
Finally! Remember that b was the y-coordinate of point A, which is also the height of \(\triangle ABC\). Now, we can finally find the area of the triangle.
\(A_{\triangle ABC}=\frac{1}{2}*18*12\\ A_{\triangle ABC}=108 \)
That's it! We are done.