heureka

Consider the line with equation
$\large (2-i)z + (2+i)\overline{z} = 20.$

For each complex number in the following list,
$\large 2,\ 4+2i,\ 3i,\ 1-4i,\ 5,\ 3,\ 10i,$

figure out whether each one is on the line.

$\text{Let $z = a+bi$} \\ \text{Let $\overline{z} = a-bi$}$

$\begin{array}{|rcll|} \hline (2-i)z + (2+i)\overline{z} &=& 20 \quad & | \quad z = a+bi, \ \overline{z} = a-bi \\ (2-i)(a+bi) + (2+i)(a-bi) &=& 20 \\ 2a+2bi-ia-bi^2 +2a -2bi +ia -bi^2 &=& 20 \\ 2a-bi^2 +2a -bi^2 &=& 20 \\ 4a-2bi^2 &=& 20 \quad & | \quad i^2 = -1 \\ 4a+2b &=& 20 \quad & | \quad : 2 \\ \mathbf{2a+b} &\mathbf{=}& \mathbf{10} \\ \hline \end{array}$

$\begin{array}{|l|l|c|l|c|} \hline &\text{list } z = a+bi:&& \mathbf{2a+b = 10} & \text{on the line} \\ \hline 1) & 2: & a= 2 & 2\cdot 2 + 0 \ne 10 \\ & & b= 0 \\\\ \hline 2) & 4+2i: & a= 4 & 2\cdot 4 + 2 \mathbf{= 10} & \checkmark \\ & & b= 2 \\\\ \hline 3) & 3i: & a= 0 & 2\cdot 0 + 3 \ne 10 \\ & & b= 3 \\\\ \hline 4) & 1-4i: & a= 1 & 2\cdot 1 -4 \ne 10 \\ & & b= -4 \\\\ \hline 5) & 5: & a= 5 & 2\cdot 5 + 0 \mathbf{= 10} & \checkmark \\ & & b= 0 \\\\ \hline 6) & 3: & a= 3 & 2\cdot 3 + 0 \ne 10 \\ & & b= 0 \\\\ \hline 7) & 10i: & a= 0 & 2\cdot 0 + 10 \mathbf{= 10} & \checkmark \\ & & b= 10 \\\\ \hline \end{array}$

Thank you, CPhill.

just algebra q2

$2^{2x}+7*2^x=8$

$\begin{array}{|lrcll|} \hline & 2^{2x}+7*2^x &=& 8 \\ & 2^{2x}+7*2^x -8 &=& 0 \\ & (2^x+8)(2^x-1) &=& 0 \\\\ 1. & 2^x+8 &=& 0 \\ & 2^x &=& -8 \quad x \text{ is an imaginary number},\ x = \dfrac{2 i \pi n + i \pi + 3 \ln(2)}{\ln(2)}, n \in \mathbb{ Z} \\\\ 2. & 2^x-1 &=& 0 \\ & 2^x &=& 1 \\ & 2^x &=& 2^0 \\ & \mathbf{x} & \mathbf{=} & \mathbf{0} \\ \hline \end{array}$

Von einer rechteckigen Marmorplatte ist eine Ecke abgebrochen(vgl. Abbild.).
Aus der fünfeckigen Restplatte soll durch Schnitte parallel zu den SEiten des ursprünglichen Rechtecks,
eine möglichst große rechteckige Platte herausgeschnitten werden.
Welche Maße hat diese Platte, und wie viel Prozent der ursprünglichen Plattenfläche nimmt sie ein?

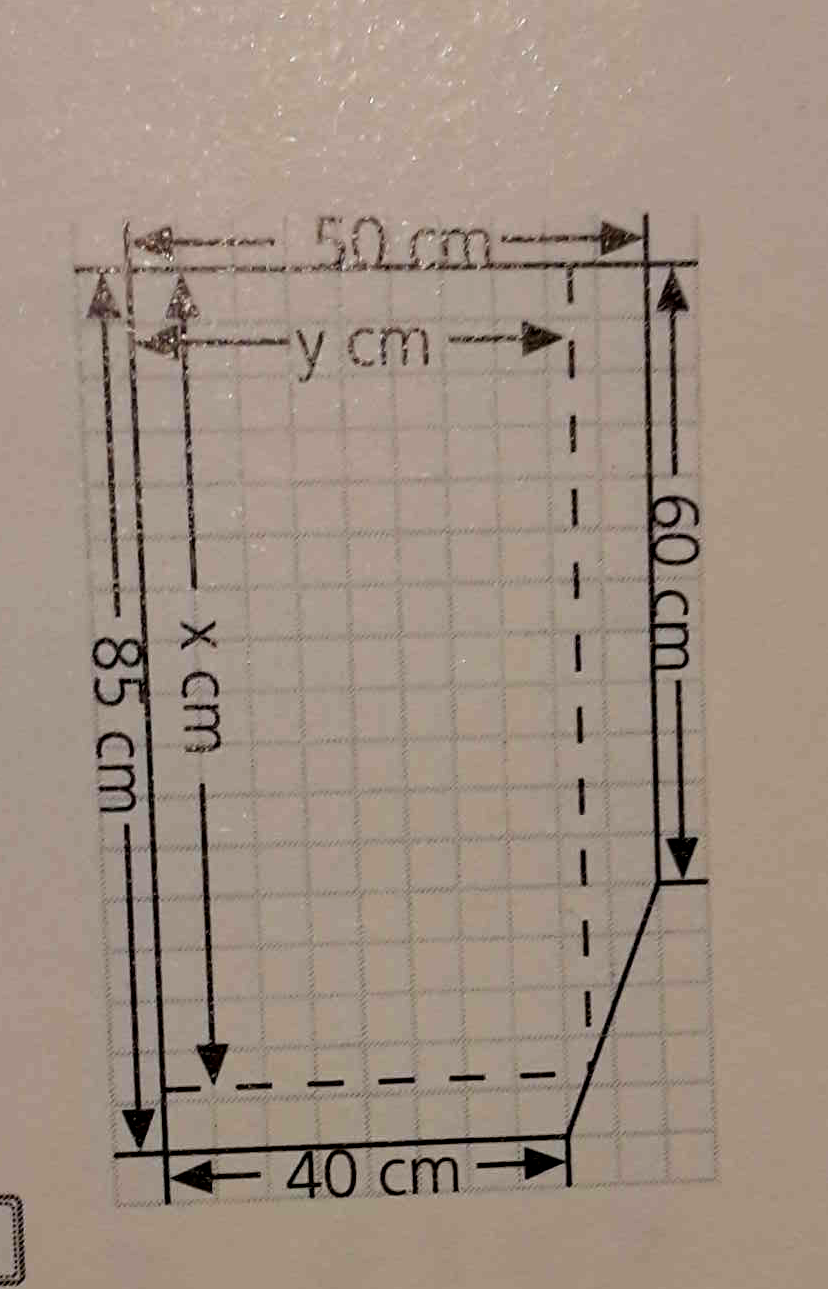
1. Hauptbedingung: Die Fläche der rechteckigen Platte A = xy

2. Nebenbedingung:

$\begin{array}{llcll} 1) & x \text{ ist nur sinnvoll im Bereich der Schrägen}, \\ & \text{daher ist der Definitionsbereich eingeschränkt auf }60\ cm \le x \le 85\ cm \\\\ 2) & \text{Strahlensatz: } \\ & \begin{array}{rcll} \dfrac{85-x}{10-(50-y)} &=& \dfrac{25}{10} \\\\ \dfrac{85-x}{y-40} &=& \dfrac{5}{2} \\\\ \text{nach $y$ aufgelöst: } \\ y &=& 74 - \dfrac{2}{5}x \\ \end{array} \end{array}$

3. Zielfunktion:

Die Terme für x und y aus den Nebenbedingungen in die Hauptbedingung einsetzen,
um die Zielfunktion zu erstellen:
$\begin{array}{rcl} A(x) &=& x\left(74- \dfrac{2}{5}x\right) \\ &=& 74x - \dfrac{2}{5}x^2 \end{array}$
Die Zielfunktion beinhaltet jetzt nur noch eine Variable, von der die Größe A abhängt.

4. Optimum (hier: Maximum):

$\begin{array}{lrcll} \text{Ableitungen bilden: } \\ & A'(x) &=& 74 - \dfrac{4}{5}x \\ & A''(x) &=& - \dfrac{4}{5} \\ \text{Extremstelle(n) ermitteln: } \\ & A'(x) &=& 74 - \dfrac{4}{5}x = 0 \quad \Rightarrow \quad x = 92.5\ (\text{Maximum}) \\ \end{array}$

Der Wert des Extremums x = 92,5 cm liegt außerhalb des zulässigen Bereiches (s.o.)
und kann damit keine Lösung sein. Daher müssen die Ränder des Definitionsbereiches
betrachtet werden, um das globale Maximum in diesem Bereich zu ermitteln:
$A(60) = 60\ cm \cdot 50\ cm = 3000\ cm^2 \qquad A(85) = 85\ cm \cdot 40\ cm = 3400\ cm^2$

Damit ist $x = 85\ cm$ und $y = 40\ cm$ die gesuchte Lösung.

Die ursprünglichen Plattenfläche war $85\ cm \cdot 50\ cm = 4250\ cm^2$

Die neue Fläche nimmt $\dfrac{3400\ cm^2}{4250\ cm^2} = 0.8\ (80 \%)$ der ursprünglichen Plattenfläche ein.

A geometric series

$b_1+b_2+b_3+\cdots+b_{10}$ has a sum of 180.
Assuming that the common ratio of that series is $\dfrac{7}{4}$,
find the sum of the seres $b_2+b_4+b_6+b_8+b_{10}$.

Geometric series:

$\begin{array}{|rcll|} \hline b_1 &=& a \\ b_2 &=& ar \\ b_3 &=& ar^2 \\ b_4 &=& ar^3 \\ b_5 &=& ar^4 \\ b_6 &=& ar^5 \\ b_7 &=& ar^6 \\ b_8 &=& ar^7 \\ b_9 &=& ar^8 \\ b_{10} &=& ar^9 \\ \mathbf{r} &=& \mathbf{ \dfrac{7}{4}} \\\\ s_{10} & = & b_1+b_2+b_3+b_4+b_5+b_6+b_7+b_8+b_9+b_{10} \\ \mathbf{s_{10}} &\mathbf{=}& \mathbf{180} \\ \hline \end{array}$

The sum of a geometric series $s_{10}$:

$\begin{array}{|rcll|} \hline s_{10} &=& a\left(\dfrac{1-r^{10}}{1-r}\right) \\ &\text{or} \\ \mathbf{a} & \mathbf{=}& \mathbf{ \dfrac{s_{10}(1-r) }{1-r^{10}} } \\ \hline \end{array}$

$\text{Let $\mathbf{x}=b_2+b_4+b_6+b_8+b_{10}$}$

$\begin{array}{|rcll|} \hline s_{10} &=& b_1+b_2+b_3+b_4+b_5+b_6+b_7+b_8+b_9+b_{10} \\\\ s_{10} &=& b_1+(b_2+b_4+b_6+b_8+b_{10})+b_3+b_5+b_7+b_9 \\\\ s_{10} &=& b_1+(b_2+b_4+b_6+b_8+b_{10})+r\left(\dfrac{b_3}{r}+\dfrac{b_5}{r}+\dfrac{b_7}{r}+\dfrac{b_9}{r}\right) \\\\ s_{10} &=& b_1+(b_2+b_4+b_6+b_8+b_{10})+r\cdot (b_2+b_4+b_6+b_8) \\\\ s_{10} &=& b_1+(b_2+b_4+b_6+b_8+b_{10})+r\cdot (b_2+b_4+b_6+b_8)+rb_{10}-rb_{10} \\\\ s_{10} &=& b_1+(b_2+b_4+b_6+b_8+b_{10})+r\cdot (b_2+b_4+b_6+b_8+b_{10})-rb_{10} \\\\ s_{10} &=& b_1+x+r\cdot x-rb_{10} \\\\ s_{10} &=& x(1+r) + b_1-rb_{10} \quad | \quad b_1 = a,\ b_{10}= ar^9 \\\\ s_{10} &=& x(1+r) + a-rar^9 \\\\ s_{10} &=& x(1+r) + a-ar^{10} \\\\ s_{10}&=& x(1+r) + a(1-r^{10}) \quad | \quad \mathbf{a = \dfrac{s_{10}(1-r) }{(1-r^{10})} } \\\\ s_{10}&=& x(1+r) + \dfrac{s_{10}(1-r) }{(1-r^{10})}(1-r^{10}) \\\\ \mathbf{s_{10}} &\mathbf{=}& \mathbf{x(1+r) + s_{10}(1-r) } \\ \hline \end{array}$

$\mathbf{x=\ ?}$

$\begin{array}{|rcll|} \hline \mathbf{s_{10}} &\mathbf{=}& \mathbf{x(1+r) + s_{10}(1-r) } \\\\ x(1+r) &=& s_{10} - s_{10}(1-r) \\ x(1+r) &=& s_{10}\Big(1 - (1-r) \Big) \\ x(1+r) &=& s_{10} (1 - 1+r ) \\ x(1+r) &=& s_{10}r \\ \mathbf{x} &\mathbf{=}& \mathbf{s_{10}\left(\dfrac{r}{1+r}\right)} \quad | \quad s_{10}=180,\ r=\dfrac{7}{4} \\ x & = & 180\cdot \left(\dfrac{\dfrac{7}{4}}{1+\dfrac{7}{4}}\right) \\\\ x & = & 180\cdot \left(\dfrac{\dfrac{7}{4}}{ \dfrac{11}{4}}\right) \\\\ x & = & 180\cdot \left( \dfrac{7}{11} \right) \\\\ \mathbf{x} &\mathbf{=}& \mathbf{\dfrac{1260}{11}} \\ \hline \end{array}$

The sum of the series $\mathbf{b_2+b_4+b_6+b_8+b_{10}}$ is $\mathbf{\dfrac{1260}{11}}$

The sum of a geometric series whose first three terms are 8000, -12000, and 18000 is 57875.

What is the last term of the series?

Geometric series:

$\begin{array}{lrcll} \text{first term} & a_1 &=& a \\ \text{second term} & a_2 &=& ar \\ \text{third term} & a_3 &=& ar^2 \\ \ldots \\ \text{last term} & a_n &=& ar^{n-1} \\\\ \text{so}& a_1 &=& 8000 \\ & a_2 &=& -12000 \\ & a_3 &=& 18000 \\\\ \text{a=?} & a &=& a_1 \\ & \mathbf{a} & \mathbf{=}& \mathbf{8000} \\\\ \text{r=?} & r &=& \dfrac{a_2}{a_1} = \dfrac{a_3}{a_2} \\ & r &=& \dfrac{-12000}{8000} \\ & \mathbf{r} & \mathbf{=}& \mathbf{-\dfrac{3}{2}} \\ \end{array}$

The sum of a geometric series $s_n$:

$\begin{array}{|rcll|} \hline s_n &=& a\left(\dfrac{1-r^{n}}{1-r}\right) \\\\ s_n &=& \dfrac{a-ar^{n}}{1-r} \\\\ s_n &=& \dfrac{a-ar^{n-1}r}{1-r} \quad | \quad a_n = ar^{n-1} \\\\ \mathbf{s_n} & \mathbf{=}& \mathbf{\dfrac{a-a_nr}{1-r} } \\ \hline \end{array}$

The last term $a_n$:

$\begin{array}{|rcll|} \hline s_n &=& \dfrac{a-a_nr}{1-r} \\ s_n(1-r) &=& a-a_nr \\ a_nr &=& a-s_n(1-r) \\ a_n &=& \dfrac{ a-s_n(1-r) } {r} \quad & | \quad a=8000,\ s_n =57875, \ r =-\dfrac{3}{2} \\ a_n &=& \dfrac{ 8000-57875\left(1-\left(-\dfrac{3}{2}\right)\right) } {-\dfrac{3}{2}} \\ a_n &=& -\dfrac{2}{3}\cdot \left( 8000-57875\cdot \dfrac{5}{2} \right) \\ a_n &=& \dfrac{1}{3}\cdot \left( 5\cdot 57875-16000 \right) \\ a_n &=& \dfrac{273375}{3} \\ \mathbf{a_n} & \mathbf{=}& \mathbf{91125} \\ \hline \end{array}$

The last term of the series is 91125

Thank you, CPhill

We roll a fair 6-sided die 5 times.
What is the probability that exactly 3 of the 5 rolls are either a 1 or a 2?

$\begin{array}{|rcll|} \hline && \dbinom{5}{3}\left(\dfrac{2}{6}\right)^3\left(\dfrac{4}{6}\right)^2 \\\\ &=& \dbinom{5}{3}\left(\dfrac{1}{3}\right)^3\left(\dfrac{2}{3}\right)^2 \\\\ &=& \dfrac{5}{3}\cdot\dfrac{4}{2}\cdot\dfrac{3}{1}\cdot \dfrac{1}{3^3}\cdot \dfrac{4}{3^2} \\\\ &=& 10\cdot \dfrac{4}{3^5} \\\\ &=& 10\cdot \dfrac{4}{243} \\\\ &=& \dfrac{40}{243} \\\\ &=& 0.16460905350\ (16.5 \%) \\ \hline \end{array}$

Inverse

1.
$\begin{array}{|rcll|} \hline g(f(x)) & \overset{?}{=} & x \quad | \quad f(x) = -\dfrac{1}{4}x + \dfrac{1}{4} \\ g(-\dfrac{1}{4}x + \dfrac{1}{4} ) & \overset{?}{=} & x \\ -4\left( -\dfrac{1}{4}x + \dfrac{1}{4} \right) +1 & \overset{?}{=} & x \\ x-1+1 & \overset{?}{=} & x \\ x & \overset{!}{=} & x \quad \text{the functions are inverses }\\ \hline \end{array}$

2.
$\begin{array}{|rcll|} \hline g(f(x)) & \overset{?}{=} & x \quad | \quad f(x) = \dfrac{5x+20}{8} \\ g(\dfrac{5x+20}{8}) & \overset{?}{=} & x \\ \dfrac{-20+8\left( \dfrac{5x+20}{8} \right) }{5}& \overset{?}{=} & x \\ -4 + \dfrac{5x+20}{5} & \overset{?}{=} & x \\ -4 + x + 4 & \overset{?}{=} & x \\ x & \overset{!}{=} & x \quad \text{the functions are inverses }\\ \hline \end{array}$

 If $\bold{a}$ and $\bold{b}$ are vectors such that $\|\bold{a}\| = 4$, $\|\bold{b}\| = 5$, and
 $\|\bold{a} + \bold{b}\| = 7$, then find $\|2a-3b\|$

If a and b are vectors such that $||a||=4$, $||b||=5$, and $||a+b||=7$, then find $||2a-3b||$.

1.) trigonometric
$x = ||2\vec{a}-3\vec{b}||$

$\begin{array}{|rcll|} \hline 7^2 &=& 4^2+5^2- 2*4*5*\cos(A) \\ 49 &=& 16+25- 40\cos(A) \\ 40\cos(A) &=& 16+25-49 \\ 40\cos(A) &=& -8 \\ \mathbf{\cos(A)} &\mathbf{=}& \mathbf{-\dfrac{1}{5}} \\\\ x^2 &=&(2\cdot 4)^2+(3\cdot 5)^2-2*8*15*\cos(180^{\circ}-A )\\ x^2& =&8^2+15^2-16*15*\cos(180^{\circ}-A )\\ x^2&=& 64+225 + 240*\cos(A) \\ x^2&=& 289 + 240*\left(-\dfrac{1}{5}\right) \\ x^2&=& 289 - 48 \\ x^2&=& 241 \\ \mathbf{x }&\mathbf{=}& \mathbf{\sqrt{241 }} \\ \hline \end{array}$

2.) vectorial

$\text{Let $\vec{a}=\dbinom{x_a}{y_a} $ } \\ \text{Let $\vec{b}=\dbinom{x_b}{y_b} $ } \\ \text{Let $\vec{a}\cdot \vec{b}= x_a\cdot x_b+y_a\cdot y_b $ } \\ \text{Let $\vec{a}+\vec{b}=\dbinom{x_a+x_b}{y_a+y_b} $ } \\ \text{Let $2\vec{a}-3\vec{b}=\dbinom{2x_a-3x_b}{2y_a-3y_b} $ }$

$\begin{array}{|rcll|} \hline ||\vec{a}+\vec{b}|| &=& 7 \\ ||\vec{a}+\vec{b}||^2 &=& 7^2 \\ ||\vec{a}+\vec{b}||^2 &=& 49 \quad | \quad ||a+b||^2 = (x_a+x_b)^2 + (y_a+y_b)^2 \\ (x_a+x_b)^2 + (y_a+y_b)^2 &=& 49 \\ x_a^2 +2x_ax_b+x_b^2 + y_a^2 + 2y_ay_b+y_b^2 &=& 49 \\ x_a^2+y_a^2+x_b^2+y_b^2 +2(x_ax_b+ 2y_ay_b) &=& 49 \quad | \quad x_a^2+y_a^2 = ||\vec{a}||^2=4^2=16 \\ 16+x_b^2+y_b^2 +2(x_ax_b+ 2y_ay_b) &=& 49 \quad | \quad x_b^2+y_b^2 = ||\vec{b}||^2=5^2=25 \\ 16+25 +2(x_ax_b+ 2y_ay_b) &=& 49 \quad | \quad x_a\cdot x_b+y_a\cdot y_b = \vec{a}\cdot \vec{b}\\ 41 +2\vec{a}\cdot \vec{b} &=& 49 \\ 2\vec{a}\cdot \vec{b} &=& 8 \\ \mathbf{\vec{a}\cdot \vec{b}} &\mathbf{=}& \mathbf{4} \\ \hline \end{array}$

$\begin{array}{|rcll|} \hline ||2\vec{a}-3\vec{b}|| &=& ||\dbinom{2x_a-3x_b}{2y_a-3y_b} || \\ ||2\vec{a}-3\vec{b}||^2 &=& (2x_a-3x_b)^2 + (2y_a-3y_b)^2 \\ &=& 4x_a^2 -12x_ax_b + 9 x_b^2 + 4y_a^2 - 12y_ay_b + 9 y_b^2 \\ &=& 4(x_a^2+ y_a^2) + 9( x_b^2+y_b^2) -12(x_ax_b + y_ay_b) \\\\ && x_a^2+y_a^2 = ||\vec{a}||^2=4^2=16 \\ && x_b^2+y_b^2 = ||\vec{b}||^2=5^2=25 \\ && x_a\cdot x_b+y_a\cdot y_b = \vec{a}\cdot \vec{b}\\ \\ &=& 4\cdot 16 + 9\cdot 25 -12\vec{a}\cdot \vec{b} \quad | \quad \vec{a}\cdot \vec{b} =4\\ &=& 64 + 225 -12\cdot 4 \\ &=& 289 - 48\\ &=& 241 \\ \mathbf{||2\vec{a}-3\vec{b}||} &\mathbf{=}& \mathbf{\sqrt{241 }} \\ \hline \end{array}$