Melody

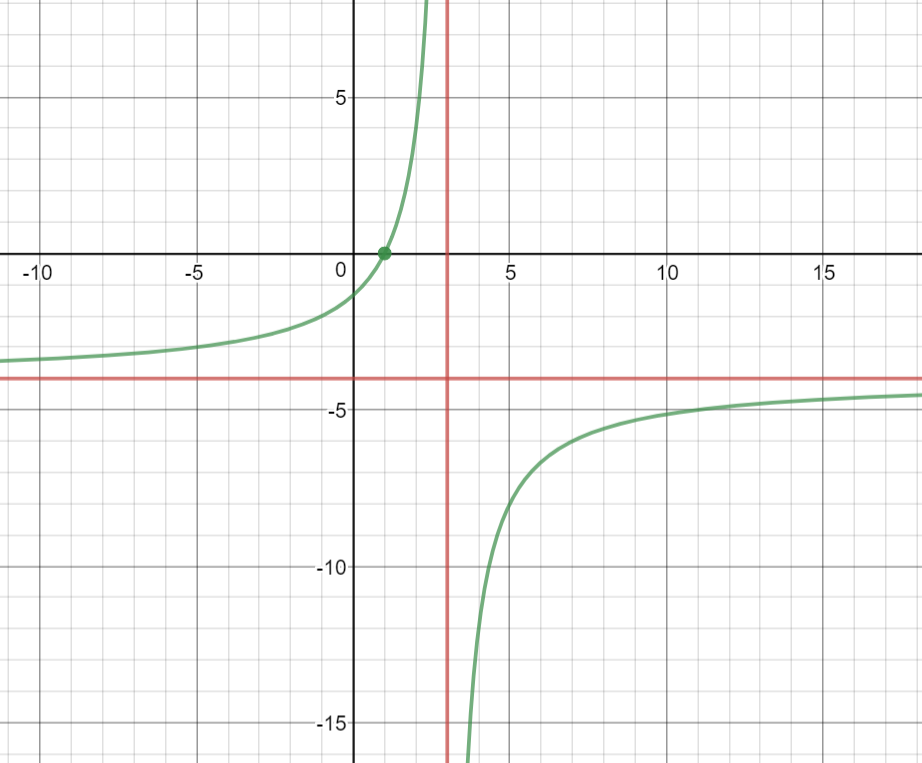
Hi,

I struggled a little to get my head around it too.   

I'm letting y=f(x) some of the time because it is easier for me to work with.

there is a vertical asymptote at x=3 this means that  y tends to =+ or - infinty when x=3

This will happen if the denominator tends to 0 as x tends to 3

hence c=-3

There is a horizontal asymptote at y=-4.

This means that as y tends to  -4,     x  tends to =+ or - infinty 

So 

  \(\displaystyle \lim_{x\rightarrow \infty}\; f(x)=-4\qquad or \qquad \displaystyle \lim_{x\rightarrow -\infty}\; f(x)=-4\\ a=-4\qquad or \qquad a=-4\\ so\;\;a=-4 \)

so we have

\(f(x) = \frac{-4x+b}{x-3}\)

Now sub in  ( 1,0) to get the value of b 

you will get b=4

\(f(x) = \frac{-4x+4}{x-3}\)

If you think about the asymptotes on a graph it might help. It did help me.

And here is the actual graph

\(\text{Sketch the graph  }\quad y= \frac{\pi}{2}\; sin^2x  \quad  \text{and use it to solve the equation  }\quad2x=\pi\;sin^2x\)

Don't apologize! I give my time freely. If I help someone learn and get a thank you then it makes me very happy.  :))

If you still are having trouble filling in the blanks I am quite happy to elaborate :)  You only have to ask :)

Good, thank you :)

Max that sounds like total nonsense.

If your teacher did not want other kids to cheat they would not want you to cheat either!

You take if off to attempt to disguise the fact that you are cheating.

It is extremely rude. People have been banned from this site for doing this.

People go to the effort of answering your question and then you blank your question. You have not even bothered to give Olpers a proper thankyou.

You have not even given him/her a point although I notice you are quite happy to give yourself a point just for asking a question.

It is not good that you have drawn attention to yourself in this way.

Do not ever delete any of your question in the future!

Here is my diagram

See if you can work it out from that. Let us know either way :)

I believe the area if 28. 

I am sorry, right now I don't have time to write it up (and hence check my own logic) 

but

I used similar triangles. 

If you let M be the midpoint of AC then   triangle AMB= triangle CMB

and they are both similar to triangle ACD

ACD is bigger by a factor of 2.

hence its area is bigger by a factor of 4

So the big one has twice the area of the 2 little ones combined

so

Area of ACD = 2/3 * 42 = 28 unites squared.

Note: this is not an answer.

Hi Daisy,

This shape is ony called a Trapezoid in USA and Canada. The rest of the English speaking world knows it as a Trapezium.

In England a Trapezoid has no parallel sides. 

To me, in Australia, a trapezoid has no meaning at all.   At least I have never known of one.

Anyway, you are referring to a quadrilateral with one pair of parallel sides.    (What I would call a Trapezium)

If you are having trouble understanding what I have done I shall try to compare it to base 10

Remember:

In base 10

\(23606 = 2*10^4+3*10^3+6*10^2+0*10+6\)

or

\(110100\\ = 1*10^5+1*10^4+0+1*10^2+0+0 \\ = 10^5+10^4+0+10^2+0+0\)