I want to find the smallest distance between \((x,\frac{x^2-8}{2}) \qquad and \qquad (0,0)\)
The distance between these is
\(d=\sqrt{(x-0)^2+(\frac{x^2-8}{2}-0)^2} \\d= \sqrt{x^2+(\frac{x^2-8}{2})^2}\)
We need to minimize that expression and solve for x
I will get the same result if I minimize
\(x^2+(\frac{x^2-8}{2})^2 \qquad or \qquad 4x^2+(x^2-8)^2\)
Let
\(T=4x^2+(x^2-8)^2\\ \frac{dT}{dx}=8x+2(x^2-8)^1*2x\\ \frac{dT}{dx}=8x+4x(x^2-8)\\ \frac{dT}{dx}=8x+4x^3-32x\\ \frac{dT}{dx}=4x^3-24x\\ \frac{dT}{dx}=4x(x^2-6)\\ \frac{dT}{dx}=4x(x-\sqrt 6)(x+\sqrt 6)\\~\\ \frac{dT}{dx}=0 \;\;\;\;when\;\;\;\;\ x=0,\;\;x=\pm\sqrt6\)
When x=0
\(d= \sqrt{x^2+(\frac{x^2-8}{2})^2}\\ d= \sqrt{16}\\ d=4 \)
When \(x=\pm\sqrt6\)
\(d= \sqrt{x^2+(\frac{x^2-8}{2})^2}\\ d= \sqrt{6+(\frac{6-8}{2})^2}\\ d= \sqrt{6+1}\\ d=\sqrt7\\ d\approx 2.64\)
So it looks to me like the min distance is when x= \(\sqrt7 \quad \text{and it occurs when }\quad x=\pm\sqrt6\)
I'll look at the second derivative for verification.
\(\frac{dT}{dx}=4x^3-24x\\ \frac{d^2T}{dx^2}=12x^2-24\\ \frac{d^2T}{dx^2}=12(x^2-2)\\ \)
When \(x=\pm \sqrt 6\\ \frac{d^xT}{dx^2}= 48>0 \quad \text{So minimum}\)
When \(x= 0\\ \frac{d^xT}{dx^2}= -24<0 \quad \text{So maximum}\)
So I get the minimum distance to be sqrt7
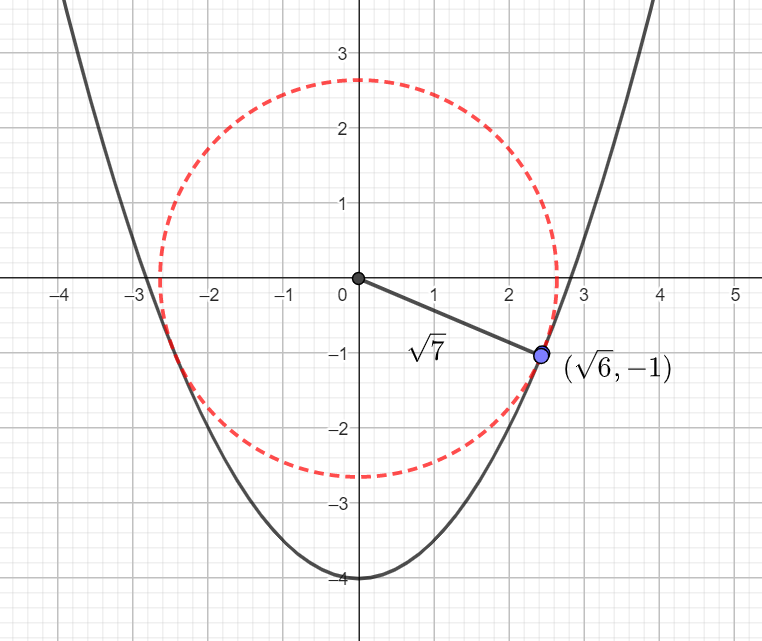
And here is the pic
LaTex:
T=4x^2+(x^2-8)^2\\
\frac{dT}{dx}=8x+2(x^2-8)^1*2x\\
\frac{dT}{dx}=8x+4x(x^2-8)\\
\frac{dT}{dx}=8x+4x^3-32x\\
\frac{dT}{dx}=4x^3-24x\\
\frac{dT}{dx}=4x(x^2-6)\\
\frac{dT}{dx}=4x(x-\sqrt 6)(x+\sqrt 6)\\~\\
\frac{dT}{dx}=0 \;\;\;\;when\;\;\;\;\ x=0,\;\;x=\pm\sqrt6