Factored/Simplified Expressions
You take an expression, find all its factors, write it out as a product of factors, you get the factored form.
You expand all the product, then you get the simplified form.
Example:
\(x^2+2x-15\qquad \text{This is}\color{blue}{\text{ simplified}}\color{black}\text{.}\\ (x+5)(x-3)\qquad \text{This is}\color{magenta}{\text{ factored}}\color{black}\text{.}\\\)
Removable discontinuity
This usually only happens when the given function is rational.
1. Find the G.C.D. of the numerator and the denominator.
2. Set the G.C.D. to 0
3. The roots of the equation in step 2 is where the removable discontinuity occurs.
Example:
Find the removable discontinuity(discontinuities) of the function \(f(x) = \dfrac{\dfrac{1}{4}x^2-x+1}{x^2-4}\).
Solution:
\(f(x)\\ =\dfrac{\dfrac{1}{4}x^2-x+1}{x^2-4}\\ =\dfrac{\dfrac{1}{4}(x^2-4x+4)}{(x-2)(x+2)}\\ =\dfrac{\dfrac{1}{4}(x-2)^2}{(x-2)(x+2)}\\ =\dfrac{(x-2)^2}{4(x-2)(x+2)}\)
GCD of numerator and denominator is (x-2). <- Set this to 0.
x - 2 = 0
x = 2
The removable discontinuity of this function occurs at x = 2.
Vertical asymptotes and horizontal asymptotes
Vertical asymptotes occurs at (unremovable) discontinuities.
Horizontal asymptotes is just a horizontal line which the function approaches when x reaches positive or negative infinity.
How to find...
Vertical asymptotes? Find all the discontinuities, exclude the removable ones and the "broken" points(like this one below, at x = 1.)
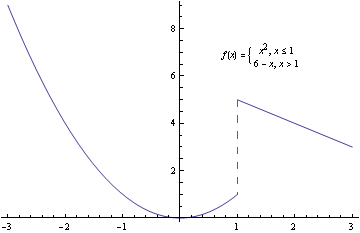
Horizontal asymptotes? That's a calculus thing. If you want to do it the algebra way, you can substitute larger and larger numbers into the function and see if the function reaches a value eventually, and then repeat with negative numbers.
Example:
Find all the horizontal and vertical asymptotes of the function y = 1/x.
Solution:
Let's find the horizontal asymptotes first. If you substitute large numbers, you will find that it approaches 0 eventually. Same for negative numbers. So the only horizontal asymptote, in this case, is y = 0.
The function has a discontinuity at x = 0, and it is not removable. So vertical asymptote is at x = 0.
Domain and range
Domain is the set of possible inputs of the function.
Range is the set of possible outputs of the function.
Example:
Find the domain and range of the function \(f(x) = \dfrac{1}{\sqrt{x-5}}\).
Solution:
This requires some kind of sense of mathematics. Firstly, the denominator can't be 0, or it will give infinity. So we have \(\sqrt{x-5} \neq 0 \implies x - 5 \neq 0\).
Also, \(\sqrt{ }\) can't take negative numbers as input. So \(x - 5 \geq 0\). But actually as the denominator can't be 0, x - 5 can't be 0. So \(x - 5 > 0\implies x > 5\).
So the domain of the function \(\text{D}\{ f(x)\} \) is \((5,\infty)\).
Now let's consider the output of the function. \(\sqrt{ }\) only gives out nonnegative numbers(0 and positive numbers if you don't know what are nonnegative numbers), So \(\sqrt{x-5} \ge 0 \implies f(x) = \dfrac{1}{\sqrt{x-5}} \le \infty\), which doesn't make any sense. But \(f(x) = \dfrac{1}{\text{a nonnegative number}}\), considering that, we get the range of f(x) as the set of all positive real numbers.
\(\text{R}\{f(x)\} \) is \((0,\infty)\).
P.S.: How do I know these without knowing all the terminologies? Google it ( ͡° ͜ʖ ͡°).