MaxWong

Simply use a calculator.

Collecting like terms,

$\begin{cases}11x - y = -14\\(a + 1)x - 5y = -11\end{cases}$

Use method of elimination, you should be able to get $x = \dfrac{59}{a - 54}, y =\dfrac{14a - 107}{a - 54}$.

It does not make sense if the denominator is 0, because you can't divide by 0. Then the system has no solutions when the denominator is 0. Can you continue from here?

Since xy - z = xz - y = 15, $(xy - z) - (xz - y) = 15 -15 = 0$.

Then $x(y - z) + (y - z) = 0$.

Factorizing gives $(x + 1)(y - z) = 0$.

Since x is positive, it is not possible that x + 1 = 0. The only possibility is y - z = 0, which implies y = z.

Similarly, we can get x = z from equation 1 and equation 3. Therefore, $x = y = z$.

Substituting that into xy - z = 15 gives $x^2 - x = 15$. You can solve it and get the positive value of x. Then since x = y = z, xyz is just x^3. Please try to continue from here.

The sum, written in sigma notation, is $\newcommand{\dsum}{\displaystyle\sum} \dsum_{k = 1}^{\infty} \dfrac2{k(k + 1)(k + 2)}$.

We can perform partial fractions to get a telescoping sum.

Note that $\newcommand{\dsum}{\displaystyle\sum} \dsum_{k = 1}^\infty (f(k) - f(k + 1)) = f(1) - \lim_{k\to\infty} f(k)$ for any function f.

Let $\dfrac2{k(k + 1)(k + 2)} = \dfrac A{k} + \dfrac B{k + 1} + \dfrac C{k + 2}$ for some constants A, B, C.

Multiplying both sides by k(k + 1)(k + 2) gives $2 = A(k + 1)(k + 2) + Bk(k + 2) + Ck(k + 1)$.

Substituting k = 0, k = -1, and k = -2 respectively gives $\begin{cases}2A = 2\\-B = 2\\2C = 2\end{cases}$.

Then A = C = 1, B = -2.

We have:

$\newcommand{\dsum}{\displaystyle\sum} \begin{array}{rcl} \dsum_{k = 1}^{\infty} \dfrac2{k(k + 1)(k + 2)} &=& \dsum_{k = 1}^\infty \left(\dfrac1k + \dfrac1{k + 2} - \dfrac2{k + 1}\right)\\ &=& \dsum_{k = 1}^\infty \left(\dfrac1k - \dfrac1{k + 1}\right) - \dsum_{k = 1} ^\infty\left( \dfrac1{k + 1} - \dfrac1{k + 2}\right) \end{array}$

Can you continue with my hints here?

Note that $f''(x) = \dfrac{d}{dx} f'(x)$.

Then $\dfrac{d}{dx} f'(x) = 4x - 2$.

Integrate on both sides, we have $f'(x) = 2x^2 - 2x + C$ for some real constant C. (Exercise: Try to write out the integration process on your own.)

Since f'(-2) = 3, we know that

$2(-2)^2 - 2(-2) + C = 3\\ C = -9$

Then f'(x) = 2x^2 - 2x - 9.

To find f(x), it is pretty much the same process, just with f''(x) replaced with f'(x) and f'(x) replaced with f(x). Please try to do that on your own.

Observe that each number in the second row is -2 times the first row.

Therefore, y = -2p. 

Use the definition directly.

f(i) + f(1) + f(-1) + f(-i)

= 2i + 1 + (-1) + (-2i)

= 0

Anthrax: thank you! 

SpaceXGeek:

As Melody mentioned, the main point of this solution is for you to learn something. 

If I give you a similar problem, would you be able to solve it?

Here's a similar problem to check your understanding:

Suppose we have positive integers a, b, c such that $\begin{cases}3ab + bc + ca \equiv 9abc\pmod{11}\\ab + 3bc + ca \equiv abc\pmod{11}\\ab + bc + 3ca \equiv 10abc \pmod{11}\end{cases}$, then can you find the remainder when a + b + c is divided by 11?

Remarks and some hints: When you only have ab, bc, ca and abc in an equation (or congruence, in this case), it is sometimes useful to consider 1/a, 1/b, 1/c. Here, I had to make sure that 1/a, 1/b, and 1/c "makes sense" under mod 13, so I pointed out that 13 is a prime. The simplification step is actually Gaussian elimination, if you have learnt linear algebra. Otherwise, you can use method of elimination to solve it. You can invert an integer a mod p by calculating $a^{-1} \equiv a^{p - 2}\pmod p$. This congruence comes from Fermat's little theorem. 

Suppose that x red marbles and y white marbles were transferred to Box B.

$\begin{cases}\dfrac{200-x}{90-y} = \dfrac11\\\dfrac{80+x}{100+y} = \dfrac32\end{cases}$

You can simplify this:

$\begin{cases}x - y = 110\\2x - 3y = 140\end{cases}$

Then solve it with any method you like:

$x = 190, y = 80$

Therefore, a total of 270 marbles were transferred.

Exercise: Try to fill in the details and present it carefully and nicely.

Let $\Omega = \{(x, y, z) : -1\le x \le 1, -1 \le y \le 1, -1\le z \le 1\}$.

Note that $\operatorname{Vol}(\Omega) = 2^3 = 8$ since it is a cube of side length 2, where Vol denotes the volume.

Now, we find the volume of the region $\Omega' = \{(x,y,z) : (x,y,z)\in\Omega, x + y + z \le1\}$.

$\dfrac{\operatorname{Vol}(\Omega')}{\operatorname{Vol}(\Omega)}$ is the required probability.

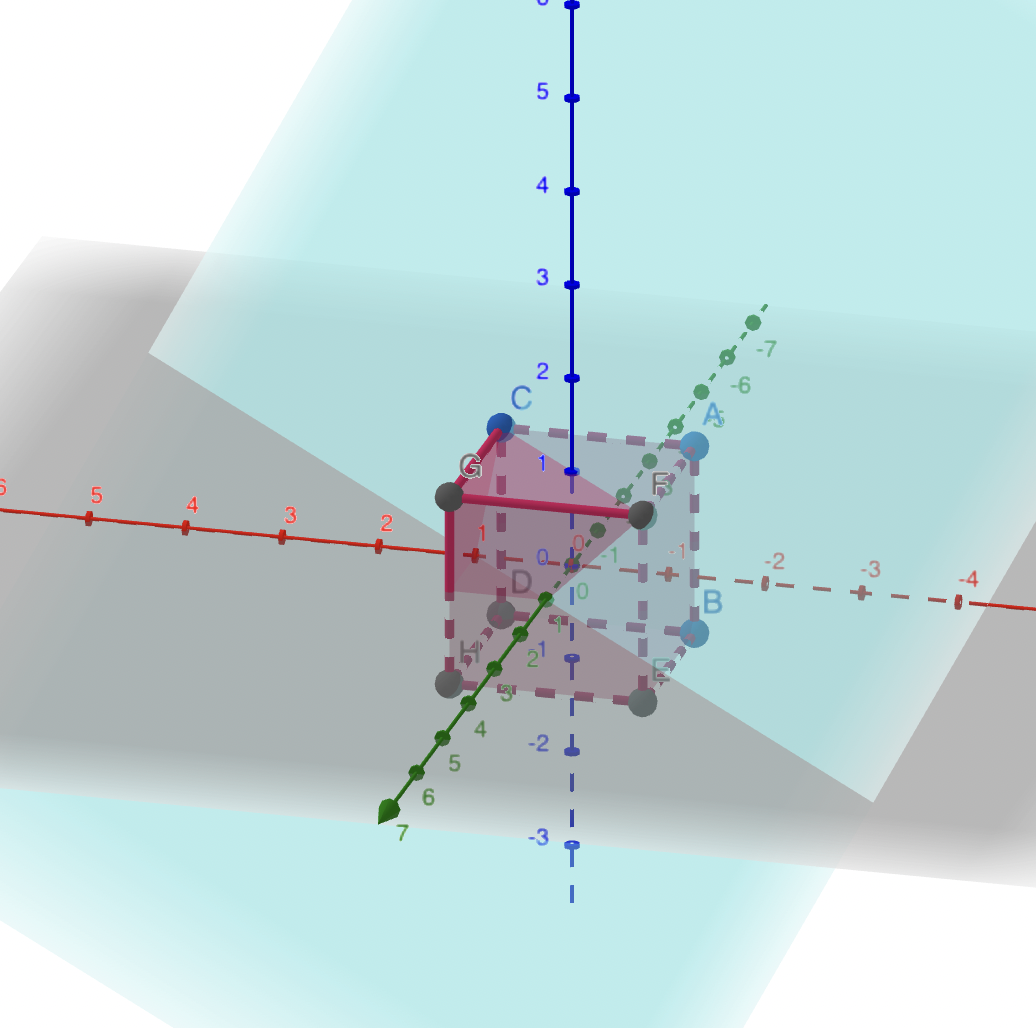
Looking at the diagram, the plane x + y + z = 1 cuts out a tetrahedron with vertices C, F, G, H, which is 1/6 of the volume.

$\newcommand{\Vol}{\operatorname{Vol}} \Vol(\Omega') = \dfrac56 \Vol(\Omega)$.

Then, $\newcommand{\Vol}{\operatorname{Vol}} \text{Prob.} = \dfrac{\Vol(\Omega')}{\Vol(\Omega)} = \dfrac56$.