Melody

Please just put one question per post.

It is amazing that you got any answer at all.  Your questions are all run together and barely readable.

This is how they shouold have been presented, only in 2 different posts.

1. Let x and b be positive real numbers so that     \(\log_b(x^2) = 10 \).

Find \(\log_{\sqrt[3]{b}} \left( \frac{1}{x} \right). \)

2. Let a, b, and c be the roots of        \(24x^3 - 121x^2 + 87x - 8 = 0\).

Find           \(\log_3(a)+\log_3(b)+\log_3(c) \).

You are always welcome. :)

I could see straight off that it wasn't an AP becasue of the power., 

You will get more used to seeing such hints too. 

Hi Juriemagic,

\(\displaystyle \sum _{k=1}^m\;\;2^{8-k}=255.5\)

First I did a little spreadsheet to see if it worked

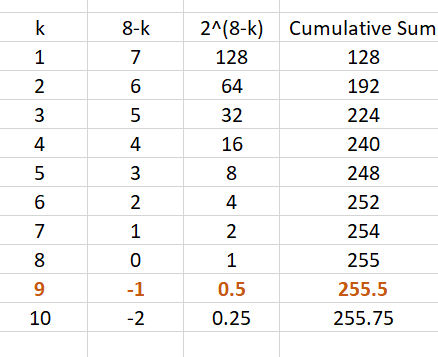
You can see that the answer is 9.

Now I will try it without the help of Excel.

The sequence is      128, 64, 32, 16 ,....

This is a GP with r=-0.5 and a=128

\(S_n=\frac{a(1-r^n)}{1-r}\\ S_n=\frac{128(1-(0.5)^n)}{0.5}=255.5\\~\\ 256(1-(0.5)^n)=255.5\\~\\ 1-(0.5)^n=\frac{255.5}{256}\\~\\ 1-\frac{255.5}{256}=(0.5)^n\\~\\ \frac{0.5}{256}=\frac{1}{2^n}\\~\\ \frac{1}{512}=\frac{1}{2^n}\\~\\ 2^n=512\\~\\ n=9 \)

Yes I think you're right.  Thanks for pointing that out guest  

Here is the desired pic

Use similar triangles to solve for x

Say we have red R and blue B

RRR

RRB

RBB

BBB

I think that is it.

Nevermind, we are all stupid sometimes.   

This question appears to be trivial

I don't understand the question.

\(a^2+b^2-2ab=(a-b)^2\)

Maybe that helps ???

Hi Aiden

\(\dfrac{1}{5} + \dfrac{3}{25} + \dfrac{7}{125} + \dfrac{15}{625} + \dfrac{31}{3125} + \cdots.\)

I can see that the bottom is  5^n

what about the top?

1,3,7,15,31    the didifferences between these is  2,4,8,16    each being a increasing power of 2

so the top is     2^n - 1

so we have

\(\displaystyle \sum_{n=1}^{\infty}\;\;\frac{2^n-1}{5^n}\\~\\ =\displaystyle \sum_{n=1}^{\infty}\;\;\left(\frac{2}{5}\right)^n\;\;-\;\; \displaystyle \sum_{n=1}^{\infty}\;\;\left(\frac{1}{5}\right)^n\\\)

You should be able to take it from there.

If the diameter of each is 2" and the total length is 1' then    12/2=6

There will be 6 semicircles on the top and 6 semicircles on the bottom which makes 6 circles

A= pi* 1^2  =  pi