Each interior angle of a regular octagon is 135o.
By Law of Cosines,
\(AC^2 = 8^2 + 8^2 - 2(8)(8)\cos135^\circ\\ AC^2 = 64\cdot \left(2 + \sqrt2\right)\\ AC = 8\sqrt{2+\sqrt 2}\)
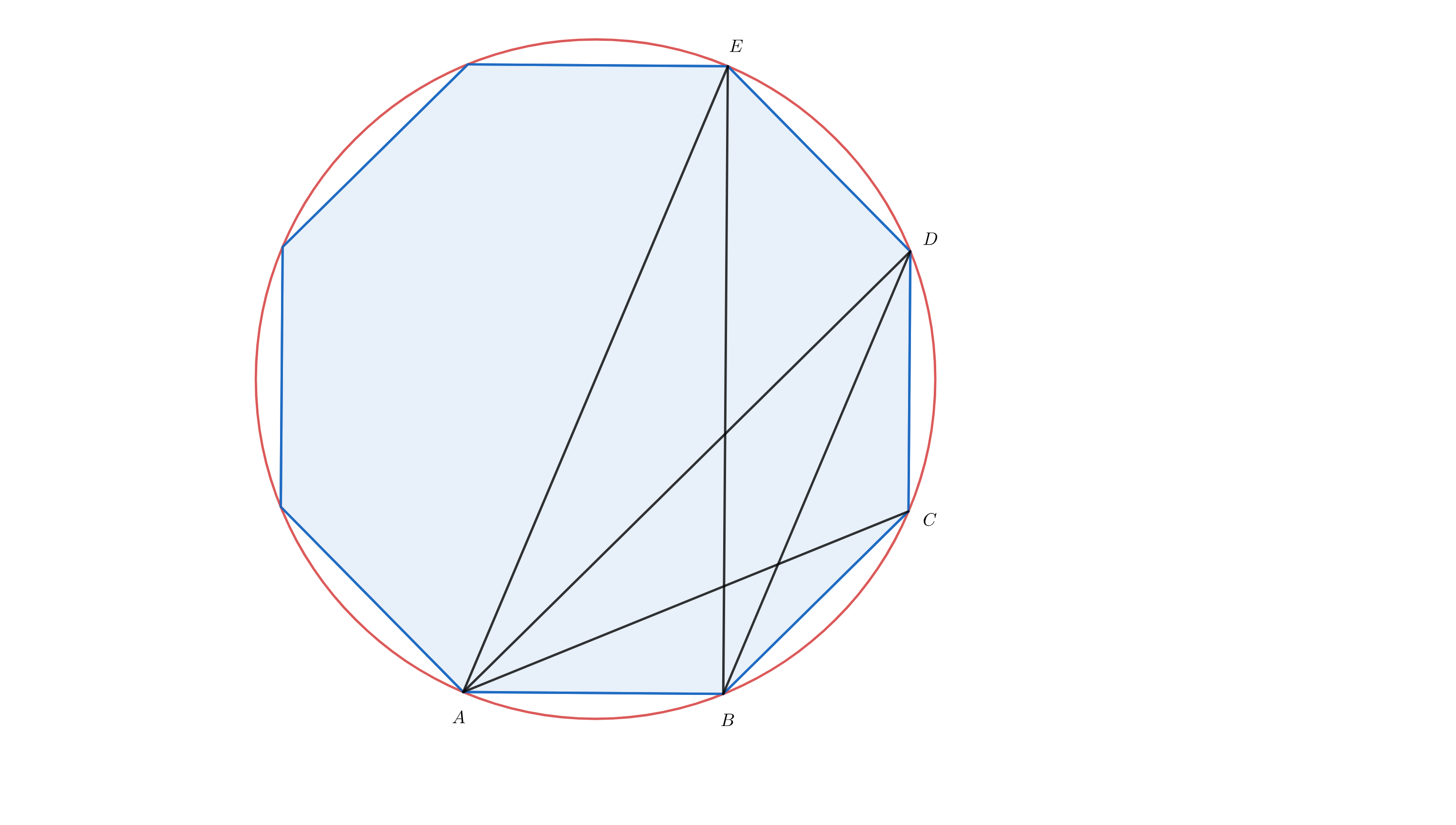
Noticing \(ABCD\) and \(ABDE\) are cyclic quadrilaterals, by Ptolemy's theorem,
\(AB\cdot CD + BC \cdot AD = AC\cdot BD\\ 8^2 + 8AD = AC^2\\ 64 + 8AD = \left(8\sqrt{2+\sqrt 2}\right)^2\\ 8 + AD = 8(2 + \sqrt 2)\\ AD = 8(1 + \sqrt 2)\)
Again by Ptolemy's theorem,
\(AB\cdot DE + BD \cdot AE = AD \cdot BE\\ 8^2 + 8\sqrt{2 + \sqrt 2}\cdot AE = (8(1 + \sqrt 2))^2\\ 8+ \sqrt{2 + \sqrt 2}\cdot AE = 8(3 + 2\sqrt 2)\\ \sqrt{2 + \sqrt 2}\cdot AE = 16(1 + \sqrt 2)\\ AE = \dfrac{16(1 + \sqrt 2)}{\sqrt{2 + \sqrt 2}} = 8\sqrt{4 + 2\sqrt 2}\)
.